पाइथागोरस प्रमेय (Pythagoras Theorem) के अनुसार, किसी समकोण त्रिभुज में (Right-Angle Triangle), कर्ण (Hypotenuse) का वर्ग, आधार (Base) और लम्ब (Perpendicular) के वर्ग (Square) के योग के बराबर (Equal) होता है.
पाइथागोरस प्रमेय का सूत्र |Pythagoras Formula in Hindi
(कर्ण)2 = (आधार)2 + (लम्ब)2
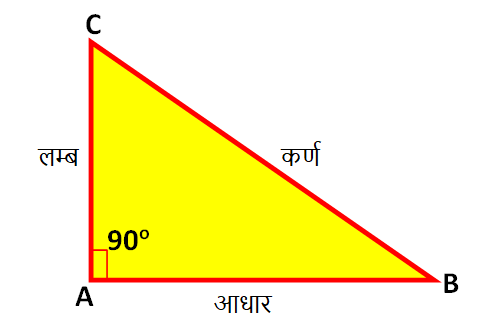
त्रिभुज ABC में, (BC)2 = (AB)2 + (AC)2
माना, त्रिभुज ABC में, कर्ण (BC) की लम्बाई 5 Cm , लम्ब की लम्बाई (AC) 4 Cm और आधार की लम्बाई (AB) 3 Cm है.
(5)2 = (3)2 + (4)2
25 = 9 + 16
25 = 25
कर्ण, लम्ब और आधार का मान (Value) रखने पर यह सिद्ध होता है की कर्ण का वर्ग, लम्ब और आधार के वर्ग के योग के बराबर होता है.
Table of Contents
पाइथागोरस थ्योरम की खोज किसने की थी? | Who Discovered Pythagoras Theorem?
पाइथागोरस प्रमेय की खोज एक महान गणितज्ञ “पाइथागोरस” ने की थी.
Also read: किरचॉफ का नियम | Kirchap Ka Niyam क्या है? | What is Kirchhoffs Law in Hindi?
पाइथागोरस प्रमेय सिद्ध करें | Pythagoras Theorem Proof
पाइथागोरस प्रमेय को सिद्ध करने के लिए, Point A से एक लम्ब (perpendicular), रेखा (line) BC पर डालते हैं.
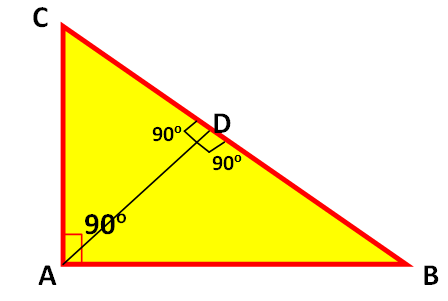
क्योंकि, त्रिभुज ABC और BDA में, कोण (Angle) B और कोण D, एक समकोण (90 डिग्री) है. यानी यह दोनों त्रिभुज ही समकोण त्रिभुज हैं.
<ABC = <BDA = 90o
<A = <A (दोनों त्रिभुजों में <A common है.)
AA Similarity के नियम के अनुसार, जब दो त्रिभुज एक समान होती हैं, तो उनकी corresponding sides का अनुपात (ratio) भी बराबर होता है.
AD /AB = AB / AC
AB × AB = AD × AC
(AB)2 = AD × AC ——————–(1)
त्रिभुज BDC और ABC में,
CD / BC = BC / AC
BC × BC = CD × AC
(BC)2 = CD × AC ———————(2)
समीकरण (1) और (2) को जोड़ने पर,
(AB)2 + (BC)2 = AD × AC + CD × AC
(AB)2 + (BC)2 = AC (AD + CD)
त्रिभुज से, AD + CD = AC
(AB)2 + (BC)2 = AC × AC
(AB)2 + (BC)2 = (AC)2 , यह समीकरण सिद्ध करती है की कर्ण का वर्ग, लम्ब और आधार के वर्ग के योग के बराबर होता है.
- What is Bernoulli’s Theorem in Hindi?
- What is Archimedes Principle in Hindi?
- What is Kirchhoff’s Law in Hindi?
- What is Ohm’s Law in Hindi?
पाइथागोरस प्रमेय का उपयोग/Application of Pythagoras Theorem in Hindi
- इस प्रमेय का उपयोग पहाड़ों के ढलवापन को ज्ञात (find out) करने के लिए किया जाता है.
- ज्यादातर, यह theorem का उपयोग, किसी बिल्डिंग को बनाते समय Architecture द्वारा किया जाता है.
- किसी समतल पर, दो बिंदुओं के बीच की दूरी को ज्ञात करने के लिए भी pythagoras प्रमेय का प्रयोग किया जाता है.
- कोई त्रिभुज एक समकोण त्रिभुज है या नहीं, यह जानने के लिए पाइथागोरस प्रमेय का उपयोग किया जाता है.
- किसी भी समकोण त्रिभुज की किसी भी भुजा (side) को पता करने के लिए यह Theorem का उपयोग किया जाता है.
- समकोण त्रिभुज (Right-angle Triangle) के कर्ण को ज्ञात करने के लिए Pythagoras Pramey का उपयोग किया जाता है.
पाइथागोरस प्रमेय का विलोम | Converse of Pythagoras Theorem in Hindi
Statement: यदि किसी त्रिभुज में दो भुजाओं (sides) के वर्गों का योग, तीसरी भुजा के के वर्ग (square) के बराबर (equal) है, तो वह त्रिभुज एक समकोण त्रिभुज (right angle Triangle) होता है.
सिद्ध करना है (Prove that): <B = <P = 90o
Converse of Pythagoras Theorem Proof: यह जानने के लिए त्रिभुज PQR एक समकोण त्रिभुज है या नहीं। हम एक समकोण त्रिभुज ABC बनाते हैं.
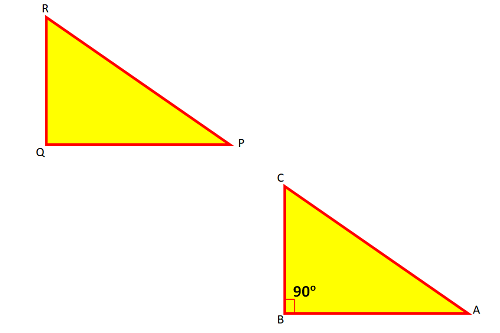
पाइथागोरस प्रमेय को समकोण त्रिभुज ABC में लगाने पर,
(AC)2 = (BC)2 + (AB)2
माना, PR = BC और PQ = BA है, तो ऊपर लिखी गई समीकरण में मान रखने पर,
(AC)2 = (PR)2 + (PQ)2 —————(3)
हम जानते हैं की, किसी भी त्रिभुज के दो sides के वर्ग का योग, तीसरी भुजा के वर्ग के योग के बराबर होता है.
ΔPQR में,
(QR)2 = (PR)2 + (PQ)2 ——————(4)
समीकरण (3) और (4) को Compare करने पर, हम देखते हैं की दायां भाग (R.H.S.) एक-दुसरे के बराबर (Equal) है, तो बायाँ भाग (L.H.S.) भी एक-दुसरे के बराबर होगा।
(AC)2 = (QR)2
AC = QR
क्योंकि, त्रिभुज PQR और ABC की तीनों भुजाएं (sides) (AC = QR, PR = BC, PQ = BA). तो, SSS के नियम के अनुसार, इनके कोण (angle) भी बराबर होंगे।
अथार्त, <B = <P = 90o
इस पोस्ट में हमने पाइथागोरस प्रमेय के बारे में पढ़ा. हमने जाना की पाइथागोरस थ्योरम की खोज कब और किसने की. और साथ ही हमने इस प्रमेय को सिद्ध किया। अब मैं चाहती हूँ की आप कुछ practice प्रश्नों को हल करें, जो मैं यहाँ लिख रही हूँ.
अक्सर पूछे जाने वाले प्रश्न | Frequently Asked Question
प्रश्न-1 किसी त्रिभुज PQR में, कोण <Q = 90o , PQ = 12cm , PR = 13cm , है, तो QR का मान ज्ञात करें। साथ ही चित्र भी बनायें।
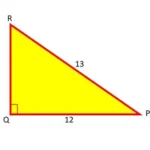
उत्तर- क्योंकि, त्रिभुज PQR एक समकोण त्रिभुज है. तो हम पाइथागोरस प्रमेय का प्रयोग करके QR की लम्बाई ज्ञात कर सकते हैं. (चित्र को देखें)
(कर्ण)2 = (लम्ब)2 + (आधार)2
(13)2 = (QR)2 + (12)2
169 = (QR)2 + 144
(QR)2 = 169- 144
(QR)2 = 25
(QR)= √25
QR = 5cm
प्रश्न-2 बौधायन प्रमेय क्या है?
उत्तर- पाइथागोरस प्रमेय को ही बौधायन प्रमेय कहते हैं.
प्रश्न-3 पाइथागोरस प्रमेय का सूत्र लिखिए।
उत्तर- (कर्ण)2 = (लम्ब)2 + (आधार)2
पाइथागोरस प्रमेय से जुड़ा अगर आपका कोई प्रश्न हैं, तो आप कमेंट बॉक्स में लिख सकते हैं या हमें email कर सकते हैं.
